对称性对于电力网络同步至关重要

东京工业大学(东京工业大学)和北卡罗来纳州立大学的联合研究小组澄清了实现电网中发电机组[1]同步的基本原则，这对于稳定的电力供应至关重要。基于这一原理，该团队开发了一种构建电网的聚合模型的方法，该模型能够有效地分析和控制发电机组的行为(包括转子相角和连接点电压)以及与电网的复杂连接。

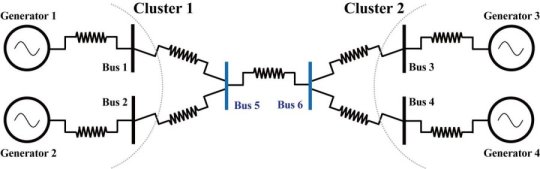
众所周知，诸如多个火力发电厂的发电机组的同步现象与稳定的电力供应密切相关。具体而言，如果发电机不同步，则该发电机及其周围的发电机将不能稳定运行，并且在最坏的情况下，可能发生诸如停电之类的严重事故。

此外，全球变暖引起的能源问题和化石燃料的枯竭在全球范围内变得更加严重。因此，从减少二氧化碳和系统使用能源的观点来看，对可再生能源的期望很高，例如以光伏(PV)发电为代表的可再生能源。当引入大规模光伏发电设备和蓄电设备时，除了当今常用的火力，液压电力和核电等发电之外，还需要考虑光伏发电输出的电力充放电。蓄电池以保持供需平衡。然而，由于根据时区天气变化和太阳辐射量变化存在不确定性，因此光伏发电产生的电量波动。这使得维护发电机组的同步变得更加困难。分析同步的需求比以往任何时候都要大。

对于传统分析，主要方法是基于数值模拟。没有研究从理论上阐明如何根据输电网络结构正确同步发电机组的基本原则。迫切需要建立有效利用电力存储设备的电力供需框架，以允许光伏发电和需求预测的不确定性。

研究成果概述

石垣孝之助教授，东京工业大学Jun-ichi Imura教授和北卡罗来纳州立大学NSF ERC FREEDM系统中心副教授Aranya Chakrabortty从多个研究开展工作，包括电网建模，稳定性分析和稳定控制。图论[2]。他们已经阐明，图论中网络的对称性是实现与电网(连接到网络)集成的火力发电厂的发电机组同步的基本原则。

通过电网中的网络连接的发电机的行为由组合微分方程和代数方程的复杂方程(微分代数方程)表示。微分方程表达了从牛顿第二运动定律导出的“发电机行为”，代数方程表达了“电网连接点的功率平衡”，这是从欧姆定律和基尔霍夫定律得出的[3]。这些微分代数方程的分析通常通过称为克朗约简的简化方法转换成数学上等效的微分方程来进行。然而，问题在于现有方法，

为了解决这个问题，他们基于对图论的理解，从对称性的角度分析了代数方程中包含的电网的网络结构。具体来说，通过分析发电机的行为而不消除代数方程，他们发现电网的对称性是实现发电机组同步的基本原则。此外，基于同时集成显示同步行为的发电机组和耦合这些发电机组的电网的新想法，可以在数学上和物理上构建可行的聚合模型。

预计该成果将为开发用于实现对大型复杂电力系统的稳定电力供应的分析和控制方法奠定基础。未来，Imura教授表示，它的目标是开发更复杂的电力系统，包括转换器，并建立一个理论来近似发电机组的同步。

注意：

[1]发电机组的同步：诸如多个发电机的涡轮机之类的转子的相角必须相同或合理地接近。每个转子根据特定频率的标准(日本为50 Hz或60 Hz)旋转，以保持其频率。每个发生器的频率差异产生相位角的差异。

[2]图论：这是一个与由顶点(节点)和边集组成的图(网络结构)相关的数学理论。电网网络被解释为连接点是顶点的图形，连接连接点的传输线是边缘。

[3]欧姆定律，基尔霍夫定律：这些物理定律表示电路中电压和电流等物理量之间的关系。欧姆定律表明电路中两点之间的电压差与它们之间的电流成正比。基尔霍夫定律表明，在电路的分支点，流向该点的电流之和等于从该点流出的电流之和。